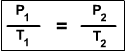EXPERIMENTO

Por ultimo, les dejamos este vídeo creado por los integrantes de este blog en el que demostramos mediante experimentos algunas de las leyes de los gases

LEY GENERAL DE LOS GASES

Combinando las leyes vistas anteriormente:

P . V = cte ( para T y m constantes):Ley de Boyle.                                                                                                      

V = cte . T (para P y m constantes): Ley de Charles y Gay-Lussac                                                                        

P = cte . T (para V y m constantes): 2ª Ley de Gay-Lussac     

Se refieren a cada una de las variables termodinámicas con relación a otra mientras todo lo demás se mantiene constante. la ley de charles establece que el volumen y la temperatura son directamente proporcionales entre sí, siempre y cuando la presión se mantenga constante. la ley de boyle afirma que la presión y el volumen son inversamente proporcionales entre sí a temperatura constante. finalmente, la ley de gay-lussac introduce una proporcionalidad directa entre la temperatura y la presión, siempre y cuando se encuentre a un volumen constante.                                                                                                  

Se obtiene la ecuación conocida como ecuación general de los gases ideales: 

Donde R es una constante denominada constante de los gases.

La presión se expresa en atmósferas,  el volumen en litros, la n es la cantidad de gas en moles,  la temperatura en K,  el valor de R es de 0,082 atm.l/mol.K,  mientras que en el S.I. el valor de R = 8,3 J / mol .K

Ley de Gas Ideal con Limitaciones

Para propósitos del cálculo, es conveniente colocar la ley de gas ideal de esta forma:

Donde los subíndices i y f se refieren a los estados inicial y final del proceso. Si limitamos la temperatura a un valor constante, esto viene a ser:

Fórmula que es llamada como la ley de Boyle.

Si la presión es constante, entonces la ley de gas ideal toma la forma

Constantes Moleculares

En la Teoría Cinética de gases, hay ciertas constantes que restringen la incesante actividad molecular.

Un determinado volumen V de cualquier gas ideal, contendrá el mismo número de moléculas. La masa del gas será pues, proporcional a la masa molecular. Una cantidad estándar de conveniencia es el mol, la masa del gas en gramos igual a la masa molecular en unidades de masa atómica (uma). El número de Avogadro es el número de moléculas en un mol de cualquier sustancia molecular.

El promedio de energía cinética de traslación, de cualquier clase de molécula en un gas ideal, está dada por

Ley de Gas Ideal

Se define como gas ideal, aquel donde todas las colisiones entre átomos o moléculas son perfectamente elásticas, y en el que no hay fuerzas atractivas intermoleculares. Se puede visualizar como una colección de esferas perfectamente rígidas que chocan unas con otras pero sin interacción entre ellas. En tales gases toda la energía interna está en forma de energía cinética y cualquier cambio en la energía interna va acompañada de un cambio en la temperatura.

Un gas ideal se caracteriza por tres variables de estado: la presión absoluta (P), el volumen (V), y la temperatura absoluta (T). La relación entre ellas se puede deducir de la teoría cinética y constituye 

n = número de moles

R = constante universal de gas = 8.3145 J/mol K

N = número de moléculas

k = constante de Boltzmann = 1.38066 x 10-23 J/K = 8.617385 x 10-5 eV/K

k = R/NA

NA = número de Avogadro = 6.0221 x 1023 /mol

La ley del gas ideal puede ser vista como el resultado de la presión cinética de las moléculas del gas colisionando con las paredes del contenedor de acuerdo con las leyes de Newton. Pero también hay un elemento estadístico en la determinación de la energía cinética media de esas moléculas. La temperatura se considera proporcional a la energía cinética media; lo cual invoca la idea de temperatura cinética. Un mol de gas ideal a TPE (temperatura y presión estándares), ocupa 22,4 litros.

TEORIA DE CHARLES Y GAY-LUSSAC

Charles y Gay-Lussac  investigaban la dilatación  del aire y otros gases, es decir, el efecto que produce el cambio de la temperatura en el volumen de una cantidad dada de aire manteniendo la presión constante

Encontraron que el gas se expandía al calentarse de forma uniforme; así, por cada grado de aumento de la temperatura, el aumento de  volumen del gas es de 1/273 veces su volumen a 0 ºC         (figura a)

La presión de un gas es directamente proporcional a la temperatura absoluta del gas e  inversamente proporcional al volumen del  recipiente.

"Para una determinada cantidad (masa) de un gas que se mantiene a presión constante, el volumen es directamente proporcional a su temperatura en la escala Kelvin".

Una forma conveniente de escribir la ley de Charles y Gay-Lussac para comparar la misma muestra de gas, a presión constante, bajo diferentes condiciones de volumen y  temperatura es:            

2ª LEY DE GAY-LUSSAC: PRESION Y TEMPERATURA

Gay-Lussac también estudió el efecto que produce en la presión el cambio de la  temperatura de una cantidad dada de aire manteniendo el volumen constante. Encontró que la presión del gas aumentaba uniformemente al calentarse.

 Si la temperatura se expresa en ºC se obtiene una función lineal como muestra la figura a, mientras que si se expresa en K, se observa que la presión es directamente proporcional a la temperatura absoluta (figura b).  

Figura B

                                                                                                                

                 

Ley de Gay-Lussac

Fue enunciada por Joseph Louis Gay-Lussac a principios de 1800.

Establece la relación entre la temperatura y la presión de un gas cuando el volumen es constante.

Al aumentar la temperatura las moléculas del gas se mueven más rápidamente y por tanto aumenta el número de choques contra las paredes, es decir aumenta la presión ya que el recipiente es de paredes fijas y su volumen no puede cambiar.

Gay-Lussac descubrió que, en cualquier momento de este proceso, el cociente entre la presión y la temperatura siempre tenía el mismo valor:

(El cociente entre la presión y la temperatura es constante)

Supongamos que tenemos un gas que se encuentra a una presión P1 y a una temperatura T1 al comienzo del experimento. Si variamos la temperatura hasta un nuevo valor T2, entonces la presión cambiará a P2, y se cumplirá:

Que es otra manera de expresar la ley de Gay-Lussac.

Esta ley, al igual que la de Charles, está expresada en función de la temperatura absoluta. Al igual que en la ley de Charles, las temperaturas han de expresarse en Kelvin.

LEY DE BOYLE

Robert Boyle fue la primera persona la cual estudió este tipo de procesos, en 1660 observó que si mantenemos constante la masa y la temperatura de un gas, al provocar variaciones en la presión que se ejerce en éste, forzosamente provocaremos variaciones en su volumen

SISTEMAS EN LOS CUALES SE APLICA LA LEY DE BOYLE MARIOTTE DENTRO DE LOS VEHICULOS

EXPERIMENTO DE BOYLE

Introdujo un gas en un cilindro con un émbolo y comprobó las distintas presiones al bajar el émbolo.                                                                                                                                      A continuación hay una tabla que muestra algunos de los resultados que obtuvo:

Si se observan los datos de la tabla se puede comprobar que al disminuir el volumen,  la presión , aumenta

En otras palabras, lo que Boyle encontró es que:                                                             

"Para una determinada masa de gas el volumen es  inversamente proporcional a la presión ejercida, si la temperatura se mantiene constante:

Se puede enunciar también de la siguiente forma:

                                                                                             

  "Para una misma masa de un gas a temperatura constante el producto del volumen del gas  por la presión que ejerce es constante"   

Esta relación es conocida como Ley de Boyle-Mariotte.

Ley de Avogadro

Esta ley, descubierta por Avogadro a principios del siglo XIX, establece la relación entre la cantidad de gas y su volumen cuando se mantienen constantes la temperatura y la presión.

Si amentamos la cantidad de gas. Esto quiere decir que al haber mayor número de moléculas aumentará la frecuencia de los choques con las paredes del recipiente lo que implica (por un instante) que la presión dentro del recipiente es mayor que la exterior y esto provoca que el émbolo se desplace hacia arriba inmediatamente. Al haber ahora mayor distancia entre las paredes (es decir, mayor volumen del recipiente) el número de choques de las moléculas contra las paredes disminuye y la presión vuelve a su valor original.

Podemos expresar la ley de Avogadro así:

(El cociente entre el volumen y la cantidad de gas es constante)

Supongamos que tenemos una cierta cantidad de gas n1 que ocupa un volumen V1 al comienzo del experimento. Si variamos la cantidad de gas hasta un nuevo valor n2, entonces el volumen cambiará a V2, y se cumplirá:

  Que es otra manera de expresar la ley de Avogadro.

  

Movimiento Browniano

A continuación les dejamos este vídeo en donde se puede ver claramente en que consiste el movimiento Browniano el cual hemos estado mencionado.

Importancia del movimiento Browniano

El movimiento browniano ha sido fuente de luz sobre otro tipo de fenómenos que ocurren en la naturaleza, dio lugar a resolver de una vez por todas la disputa que existía, en los  medios científicos de fines del siglo pasado, acerca de la estructura de la materia.

Asimismo, por tratarse inherentemente de un proceso irreversible, proporcionó uno de los primeros casos cuya evolución se pudo estudiar con todo detalle. Es importante mencionar que, para poder realizar este programa, fue necesario establecer las herramientas matemáticas adecuadas. Dado que para la descripción del fenómeno era indispensable tratar con cantidades estocásticas, se tuvo que desarrollar la teoría matemática de las funciones no-diferenciables.

El estudio microscópico del movimiento browniano proporcionó otra posibilidad, a saber, estudiar el fenómeno a muy bajas temperaturas. En este caso, es necesario utilizar la mecánica cuántica para la descripción y como consecuencia se encuentran otros tipos de comportamiento que no hubiera sido posible hallar fenomenológicamente. Por ejemplo, se descubrió la persistencia de las fluctuaciones, que es un fenómeno que apenas se está estudiando hoy día y sobre el cual aún hay mucho que aprender.

Otras facetas del movimiento browniano se encuentran en diversas situaciones físicas que tienen gran importancia, no sólo conceptual, sino de aplicación práctica como son los coloides.

Se han aplicado las ideas y métodos generados en las investigaciones sobre movimiento browniano al estudio de otros fenómenos, que son físicamente distintos, pero que tienen características muy parecidas. Uno de estos sistemas es el láser, cuya importancia no se puede subestimar. A pesar de que obviamente un láser y una partícula browniana a baja temperatura son sistemas físicos distintos, resulta que tienen propiedades estadísticas análogas y, por tanto, las técnicas de análisis desarrolladas para el segundo sistema se pueden aplicar al primero.

Modelo matemático del movimiento browniano

La exposición matemática de esta definición corresponde a  la función probabilística de densidad asociada con la ecuación de difusión de una partícula browniana, y en definitiva es una ecuación diferencial parcial.

La evolución temporal de la posición de una partícula browniana en sí misma puede ser descrita aproximadamente por una ecuación de Langevin, la cual involucra un campo de fuerzas aleatorias que representan el efecto de fluctuaciones termales de una solución de partículas brownianas. En grandes escalas de tiempo, el movimiento browniano matemático se describe perfectamente con la ecuación de Langevin. A tiempos cortos, los efectos de la inercia prevalecen en esta ecuación. Sin embargo, se considera a esta ecuación, de otra manera la ecuación se vuelve singular, así que se debe eliminar el término de la inercia de esta ecuación para tener una descripción exacta, pero el comportamiento singular de estas partículas no se describe del todo.

Otras maneras de conseguir su modelo matemático consideran un movimiento browniano

como un proceso de Gauss central con una función covariante para toda   El resultado de un proceso estocástico se le atribuye a Norbert Wiener quien dio la primera definición matemática rigurosa del movimiento quedó demostrado en la teoría de probabilidad, existente desde 1923, y se conoce con el nombre de proceso de Wiener. Él y Paul Lévy elaboraron el modelo que supone una partícula que en cada instante se desplaza de manera independiente de su pasado: es como si la partícula «olvidara» de dónde viene y decidiese continuamente, y mediante un procedimiento al azar, hacia dónde ir. O sea que este movimiento, a pesar de ser continuo, cambia en todo punto de dirección y de velocidad. Tiene trayectoria continua, pero no tiene tangente en ningún punto. Las dos propiedades básicas que Wiener supuso son: 

-Todas las trayectorias deben ser continuas.
-Una vez que fue observada la posición de la partícula en el instante t=0 (posición por tanto conocida), su posición (aleatoria) en un instante posterior t´ debe estar regido por la ley de Gauss, cuyos parámetros dependen del tiempo t transcurrido.

Figura 1. En el sistema partícula browniana-fluido cada una de las partículas componentes interacciona con todas las demás. En la figura solamente se indican algunas de estas interacciones.

Historia del movimiento browniano.

Robert Brown fue hijo de un pastor protestante escocés. Nacido en 1773 , Estudió medicina en Edimburgo y trabajó unos años como ayudante de un cirujano en un regimiento de Fifeshire.

En 1798 hizo una visita a Londres donde conoció al gran botánico Sir Joseph Banks, en aquel momento presidente de la Royal Society. Nuestro hombre lo impresionó de tal manera que tres años después hizo, con la recomendación del mismo Banks, un largo viaje a Australia regresando en 1805 con cerca de 4.000 especímenes de plantas exóticas pulcramente guardadas en el barco.

Brown es conocido, sobre todo, por un estudio de los granos de polen de la Clarkia pulcella, una flor silvestre popular actualmente entre los jardineros, descubierta en 1806 por Meriwther Lewis, aunque le puso el nombre de su compañero de exploración: William Clark. Brown pretendía analizar minuciosamente la forma y tamaño de los granos de polen con un microscopio. Pero se encontró con un problema: no paraban de moverse.

Aunque los granos de polen eran simples y carecían de partes móviles eran innegablemente orgánicos. Brown supuso que, al ser las partes masculinas del equipo reproductivo de una planta, también tenían ese espíritu vital que los impulsaba a moverse.

 De sus observaciones y las de otros científicos se pudieron obtener un par de conclusiones: que las partículas presentaban mayor movimiento entre más pequeñas fueran y que éste aumentaba también al incrementar la temperatura del líquido.

Ludwig Christian Wiener escribió una hipótesis en la que decía que este movimiento se podía explicar si el agua estuviera formada de átomos que chocaran por todas partes.

                    figura 1.1: Fuerzas que experimentas las partículas brownianas.

En 1905 entra en escena Albert Einstein, quien se interesó también en el movimiento aleatorio de las partículas suspendidas en agua, y se preguntó si el movimiento de una partícula lo suficientemente grande para ser observada bajo un microscopio al interactuar con el agua podría ser una prueba de la existencia de los átomos.

Einstein relacionó conceptos ya existentes y con su genialidad pudo encontrar una forma de demostrar la existencia de los átomos.

• El calor o aumento de la temperatura no es mas que la vibracion de los atomos. A mayor temperatura mayor movimiento atomico.
• Los atomos golpean a las particulas por todos lados y la suma de todas estas fuerzas mueven a las particulas en una direccion o en otra.
• Tambien dedujo que si mediamos el recorrido promedio de una particula en lugar de su recorrido real, podemos obtner el numero de avogadro, (contasnte muy utilizada en quimica)

                                                               Figura 1.2: Movimiento Browniano

                                           Formula para el movimiento browniano: Fenomeno de difusion,

                                  para el movimiento en una dimensión, siendo t el intervalo de tiempo 

                                  transcurrido y siendo D una constante llamada Constante de Difusión. 

El movimiento browniano

El movimiento browniano es el movimiento aleatorio que se observa en algunas partículas microscópicas que se hallan en un medio fluido (por ejemplo, polen en una gota de agua).

El movimiento estocástico de estas partículas se debe a que su superficie es bombardeada  incesantemente por las partículas (átomos) del fluido sometido a una agitación térmica.

Este bombardeo a escala atómica no siempre es  completamente uniforme y sufre variaciones estadísticas importantes. Así, la presión ejercida sobre los lados puede variar  ligeramente con el tiempo, y así se genera el movimiento observado. Tanto la difusión como la osmosis se basan en el movimiento browniano.

El modelo matematico
Fue Norbert Wiener en 1923 quien dio la primera definición matemática rigurosa del movimiento. Él y Paul Lévy elaboraron el modelo que supone una partícula que en cada instante se desplaza de manera independiente de su pasado: es como si la partícula «olvidara» de dónde viene y decidiese continuamente, y mediante un procedimiento al azar, hacia dónde ir. O sea que este movimiento, a pesar de ser continuo, cambia en todo punto de dirección y de velocidad. Tiene trayectoria continua, pero no tiene tangente en ningún punto. Las dos propiedades básicas que Wiener supuso son:

Todas las trayectorias deben ser continuas.
Una vez que fue observada la posición de la partícula en el instante t=0 (posición por tanto conocida), su posición (aleatoria) en un instante posterior t´ debe estar regido por la ley de Gauss, cuyos parámetros dependen del tiempo t transcurrido.

El movimiento browniano

Historia.
En 1827 un famoso botánico llamado Robert Brown observó que, cuando suspendía unos pequeños granos de polen en agua, estos presentaban un movimiento irregular. Este fenómeno fue llamado Movimiento Browniano en honor a su trabajo pionero. Brown demostró que el movimiento estaba presente en cualquier suspensión de partículas finas de vidrio y minerales, por lo que descartó cualquier origen orgánico de este movimiento.

El problema del movimiento Browniano no fue resuelto hasta que el físico alemán Albert Einstein en 1905 dio una explicación satisfactoria. Los dos puntos principales en la explicación de Einstein al problema del movimiento Browniano son:

• El movimiento es causado por los impactos frecuentes en el grano de polen de las moléculas del líquido, las cuales están en un movimiento incesante.
• El movimiento de estas moléculas es tan complicado, que su efecto en el grano de polen puede describirse solo probabilísticamente, en términos de los impactos frecuentes estadísticamente independientes.

Figura: Trayectoria irregular que sigue una partícula browniana.

Leyes de los Gases

Les dejamos este vídeo que explica todas las leyes de los gases que iremos mencionando posteriormente.

Ley de los gases reales

Un gas real, en oposición a un gas ideal o perfecto, es un gas que exhibe propiedades que no pueden ser explicadas enteramente utilizando la ley de los gases ideales. Para entender el comportamiento de los gases reales, lo siguiente debe ser tomado en cuenta: 

• Efectos de compresibilidad
• Capacidad calorífica específica variable.
• Fuerzas de Van der Waals
• Efectos termodinámicos del no-equilibrio
• Cuestiones con disociación molecular y reacciones elementales con composición variable.

La ecuación de Van der Waals modifica a la ecuación de los gases ideales tomando en cuenta el volumen ocupado por las moléculas, para que se aproxime de manera más precisa al comportamiento de los gases reales al tener en cuenta su tamaño no nulo y la atracción entre sus partículas.

Donde:

p es la presión del fluido, medido en atmósferas,

v es el volumen en el que se encuentran las partículas dividido por el número de partículas (en litros),

k es la constante de Boltzmann,

T es la temperatura, en kelvin

a' es un término que tiene que ver con la atracción entre partículas,

b' es el volumen medio excluido de v por cada partícula.

Explicación de la Ley de Graham

Les dejamos este vídeo donde se explica detalladamente en lo que consiste la ley de Graham de la cual hablamos la vez pasada