Difusión de los gases y la ley de Graham

La difusión es el proceso por el cual una substancia se distribuye uniformemente en el espacio que la encierra o en el medio en que se encuentra. De los 5 estados de la materia, los gases presentan la mayor facilidad de difusión de sus respectivas partículas, como ocurre en el aire, ya que sus moléculas tienen velocidades superiores. Las moléculas de diferentes gases tienen velocidades diferentes, a temperatura diferente, dependiendo únicamente de la presión.

Es por eso que en 1829 el químico británico Thomas Graham propone una ley en la que establece que las velocidades de difusión y efusión de los gases son inversamente proporcionales a las raíces cuadradas de sus respectivas masas molares. La cual es expresada por la siguiente fórmula: 

En donde v1 y v2 son las velocidades de difusión de los gases que se comparan y 

 y  son las densidades. Las densidades se pueden relacionar con la masa y el volumen porque 

y como los volúmenes moleculares de los gases en condiciones iguales de temperatura y presión son idénticos, es decir V1 = V2, en la ecuación anterior sus raíces cuadradas se cancelan, quedando:

La viscosidad en la energía cinética

La viscosidad es el rozamiento interno entre las capas de fluido. A causa de la viscosidad, es necesario ejercer una fuerza para obligar a una capa de fluido a deslizar sobre otra.
La capa de fluido en contacto con la lámina móvil tiene la misma velocidad que ella, mientras que la adyacente a la pared fija está en reposo. La velocidad de las distintas capas intermedias aumenta uniformemente entre ambas láminas tal como sugieren las flechas. Un flujo de este tipo se denomina laminar.
La fórmula para calcular la viscosidad es:          

¿Qué es un fluido ideal?

Un fluido ideal sale por la tubería con una velocidad  de acuerdo con el teorema de Torricelli. Toda la energía potencial disponible (debido a la altura h) se transforma en energía cinética. Aplicando la ecuación de Bernoulli podemos fácilmente comprobar que la altura del líquido en los manómetros debe ser cero.

¿Qué es un fluido viscoso?

En un fluido viscoso (figura de la derecha) el balance de energía es muy diferente. Al abrir el extremo del tubo, sale fluido con una velocidad bastante más pequeña. Los tubos manométricos marcan alturas decrecientes, informándonos de las pérdidas de energía por rozamiento viscoso. En la salida, una parte de la energía potencial que tiene cualquier elemento de fluido al iniciar el movimiento se ha transformado íntegramente en calor. El hecho de que los manómetros marquen presiones sucesivamente decrecientes nos indica que la pérdida de energía en forma de calor es uniforme a lo largo del tubo.

Difusión en la energía cinética de la materia

Experimento:

Si dejamos caer una gota de tinta en el recipiente con agua fría vemos que la tinta se difunde lentamente. Si a la vez dejamos caer una gota de tinta en el recipiente con agua caliente vemos que la tinta se mezcla con el agua con mayor rapidez.

Explicación:

Si se deja caer una gota de tinta en un recipiente con agua se observa que la tinta se difunde por el agua al cabo de un tiempo. Este fenómeno se debe al movimiento aleatorio de las moléculas de agua y se denomina difusión.

La teoría cinética considera que las moléculas de agua poseen un movimiento aleatorio que aumenta con la temperatura. Por tanto, en el recipiente con agua caliente las moléculas de agua se mueven con mayor velocidad que en el recipiente con agua fría.

Si las moléculas se mueven con mayor velocidad aumentan los choques con las partículas que forman la tinta y se produce la difusión con mayor rapidez.

https://www.youtube.com/watch?v=7Mv4bRgY3t0

Fenómenos fuera de equilibrio.

Cuál es el papel que desempeña cada molécula, su interacción con las moléculas vecinas, la evolución de este complejo molecular desde que empieza como un líquido y termina como un gas, requiere de un examen mucho más detallado.

Para ello regresamos a nuestro modelo cinético y veamos cómo se comportarían las moléculas que forman el gas si las sometemos a una perturbación externa. Recordemos el contenido básico de una de las leyes de Newton: Si un cuerpo dado no lo sometemos a la acción de una fuerza externa, o bien se mantendrá en reposo, o bien continuará moviéndose con velocidad constante.

Si ningún agente externo perturba de alguna manera las velocidades, estas, que varían continuamente por las colisiones, mantendrán una distribución que, como ya dijimos, tampoco cambiara con el tiempo.

Así, un sistema reacciona de diversas maneras dependiendo de cómo lo perturbemos.

Vale la pena mencionar que el transporte nulo de la masa, ímpetu y energía es una propiedad inherente de la distribución de velocidades de Maxwell.

Si por otra parte modificamos en alguna forma el ímpetu de las moléculas en una región con respecto a los de otra, el transporte neto de este provoca un fenómeno que se caracteriza por la viscosidad.

La distribución de velocidades en un gas.

Una de las características más sobresalientes de nuestro modelo cinético es concerniente a la forma en que hemos concebido con que velocidad, en magnitud y dirección, se mueven las moléculas  que forman el gas. No hay direcciones privilegiadas pero las velocidades; además, la magnitud de las velocidades puede variar desde cero hasta una velocidad máxima.

Hasta el momento se han encontrado 2 promedios: El de la velocidad y el del cuadrado de la velocidad.

¿Cómo distinguimos entre esos 2 promedios?

La velocidad “promedio” de cada partícula la calculamos en la misma forma que sacamos nuestro “promedio” de calificaciones en un periodo escolar: Sumamos todos los valores y dividimos entre el número total de ellas.

Los posibles valores de la velocidad están “repartidos” en las moléculas y si conocemos esta repartición podemos calcular, como la velocidad y el cuadrado de la misma.

Es muy difícil imaginar que entre todas las colisiones violentas que ocurren y el incesante bombardeo a que está sometida cada molécula, alguna de ellas puede estar en reposo.

Si ponemos en un gas, cualquiera que éste sea, encerrado en un recipiente, no se ve en qué  forma más o menos simple podemos introducir un selector de velocidades que nos vaya separando las moléculas por grupos de acuerdo a su velocidad que tengan. Sin contar que este lector interfiera con el movimiento de las moléculas y seguramente modificaría sus velocidades, lo cual no queremos que ocurra. Pero la naturaleza es generosa y nos ha proporcionado de todos los elementos necesarios para llevar a cabo esta medición.

Es bien sabido que algunos metales, al ser calentados a cierta temperatura emiten átomos que sus velocidades son arbitrarias. La emisión de estos átomos puede visualizarse como las ráfagas de una supermetralladora.

El problema es como seleccionamos balas distinguiéndolas por las velocidades. Este problema es relativamente fácil de resolver.

Nos fijamos en aquellas que puedan salir por una rendija colocada a cierta distancia del metal y que sirve de colimador. Este colimador permite el paso solamente de un grupo selecto de moléculas.

Para distinguir entre las partículas que pasan por el colimador, usamos una rueda dentada cuyas ranuras espaciadas a lo largo de la circunferencia. Si podemos hacerla girar. Cada ranura pasará por un punto fijo en el espacio a tiempos bien determinados. Si conocemos la distancia entre la rueda giratoria y la rendija podemos conocer el tiempo que le toma a un átomo de velocidad en viajar esta distancia; por lo tanto, para una velocidad dada podemos contar las partículas que pasan por los dientes de la rueda por medio de un detector.

LAS PROPIEDADES DE UN GAS EN EQUILIBRIO

Cuando examinamos las fases individualmente, se presentan en general, dos situaciones.                           En una estudiamos al sistema en la fase elegida en condiciones tales que sus propiedades no sean funciones del tiempo, esto es, que durante el intervalo de tiempo que dura el experimento para determinar una cierta propiedad, el sistema no cambie.                                                                                            En estas condiciones decimos que la propiedad medida corresponde a lo que se conoce como una característica del estado de equilibrio de dicho sistema.

Las relaciones que existen entre las diversas propiedades de sistemas en equilibrio constituye el tema central de la llamada termostática o termodinámica clásica.

En nuestro cotidiano contacto con las propiedades de los gases, hay dos variables que sistemáticamente utilizamos para caracterizarlos.

La presión: como sucede al inflar un neumático a la presión requerida, al referirnos a la presión atmosférica en un sitio determinado, al observar un manómetro que nos indique la presión del gas encerrado en un tanque, etc.

Las moléculas que componen el gas en cuestión están en movimiento continuo y chocan furiosamente entre sí y contra las paredes del recipiente que las contiene. 

Analicemos estos choques recordando que éstos son elásticos, Comencemos por el caso de una molécula que choca perpendicularmente contra una pared.

   Figura 2. Si la molécula tiene velocidad v antes de chocar e ímpetu mv después de la colisión, rebota y su ímpetu es m(-v) o sea -mv.   

La temperatura: hablamos de la temperatura del medio ambiente, la temperatura de los gases en un proceso de combustión, por ejemplo, de un motor de gasolina, etc.

Cuando hay una mayor temperatura existe un mayor movimiento molecular.

a) la presión ejercida por las colisiones moleculares en un gas es proporcional a la energía cinética promedio del gas.

b) la temperatura de un gas es proporcional a la energía cinética total del gas tomada como la suma de la energía cinética promedio de cada una de las moléculas que lo componen.

Las otras propiedades de equilibrio inherentes al modelo emanan de él en forma natural. Veamos cada una de estas cuestiones individualmente. 

Modelo Matemático de la Temperatura según la TCM

Vamos a partir de la ecuación que hemos obtenido para la presión:

Es posible comprender mejor el significado de la temperatura si escribimos la ecuación anterior como:

Comparándola con la ecuación de estado de un gas ideal:

De aquí encontramos que

Podemos despejar la energía cinética molecular como:

Puesto que 

se concluye que:

El siguiente teorema, llamado el teorema de la equipartición de la energía, establece que:

La energía de un sistema en equilibrio térmico se divide por igual entre todos los grados de libertad.

La energía cinética traslacional de N moléculas es simplemente N veces la energía promedio por molécula, entonces:

La raíz cuadrada de v2 se conoce como velocidad cuadrática media de las moléculas (rms, por sus siglas en inglés). Para la velocidad rms tenemos:

Temperatura en la TCM

En el ESTADO SOLIDO las moléculas están muy juntas y se mueven oscilando alrededor de unas posiciones fijas; las fuerzas de cohesión son muy grandes. En el ESTADO LIQUIDO las moléculas están más separadas y se mueven de manera que pueden cambiar sus posiciones, pero las fuerzas de cohesión, aunque son manos intensas que en el estado sólido, impiden que las moléculas puedan independizarse. En el ESTADO GASEOSO las moléculas están totalmente separadas unas de otras y se mueven libremente; no existen fuerzas de cohesión. 

Sí aumentamos la temperatura de un sistema material sólido, sus moléculas se moverán más rápidamente y aumentarán la distancia medía entre ellas, las fuerzas de cohesión disminuyen y llegará un momento en que éstas fuerzas son incapaces de mantener las moléculas en posiciones fijas, las moléculas pueden entonces desplazarse, el sistema material se ha convertido en líquido. 

Si la temperatura del líquido continúa aumentando, las moléculas aumentarán aún más su rapidez, la distancia media entre ellas irá aumentando y las fuerzas de cohesión van disminuyendo hasta que finalmente las moléculas pueden liberarse unas de otras, ahora el SISTEMA MATERIAL 0 conjunto de moléculas está en estado gaseoso. 

Si disminuimos la temperatura de un SISTEMA MATERIAL en estado gaseoso, disminuye la rapidez media de las moléculas y esto hace posible que al acercarse las moléculas casualmente, las fuerzas de cohesión, que siempre aumentan al disminuir la distancia, puedan mantenerlas unidas, el SISTEMA MATERIAL pasará al estado líquido. 

Si disminuye aún más la temperatura, al moverse más lentamente las moléculas, la distancia media entre ellas sigue disminuyendo, las fuerzas de cohesión aumentarán más y llegará un momento que son lo suficientemente intensas como para impedir que las moléculas puedan desplazaras, obligándolas a ocupar posiciones fijas, el SISTEMA MATERIAL se ha convertido en un sOLIDO

Presión en la teoría cinética de la materia

Un líquido contenido en un recipiente ejerce fuerzas contra las paredes de éste. Para describir la interacción entre el líquido y las paredes conviene introducir el concepto de presión, que se obtiene dividiendo la fuerza entre el área sobre la cual actúa la fuerza:

       Presión =fuerza/área

  La presión que un líquido ejerce depende de la profundidad; sin embargo, también depende de la densidad. Si te sumergieras en un líquido más denso que el agua la presión sería mayor. La presión de un líquido es exactamente igual al producto de la densidad de peso por la profundidad:

    Presión del líquido = densidad del peso × profundidad

Esta ecuación de las definiciones de presión y densidad. Imagina una superficie en el fondo de un recipiente con líquido. El peso de la columna del líquido que hay directamente arriba de esa área produce presión. Según la definición:        

Densidad de peso=peso/volumen

  Se puede expresar este peso de líquido como

Peso = densidad de peso × volumen

Donde el volumen de la columna es tan sólo el área multiplicada por la profundidad. Entonces, se obtiene

Para la presión total, a esta ecuación se debería sumar la presión debida a la atmósfera sobre la superficie del líquido.

Dicho con sencillez, la presión que ejerce un líquido contra las paredes y el fondo de un recipiente depende de la densidad y la profundidad del líquido. Si no tomamos en cuenta la presión atmosférica, a una profundidad doble, la presión del líquido contra el fondo sube al doble; a tres veces la profundidad, la presión del líquido es el triple, y así sucesivamente.

O bien, si el líquido tiene dos o tres veces la densidad, la presión del líquido es, respectivamente, dos o tres veces mayor, para determinada profundidad. Los líquidos son prácticamente incompresibles; esto es, su volumen casi no puede cambiar debido a la presión. Así excepto por los cambios pequeños producidos por la temperatura, la densidad de un líquido en particular es prácticamente igual a todas las profundidades.

Postulados de la teoría cinética de la materia

Estos son los principales postulados: 

1. Un gas consiste en un conjunto de pequeñas partículas que se trasladan con movimiento rectilíneo y obedecen las leyes de Newton. 
2. Las moléculas de un gas no ocupan volumen.
3. Los choques entre las moléculas son perfectamente elásticos (esto quiere decir que no se gana ni se pierda energía durante el choque).
4. No existen fuerzas de atracción ni de repulsión entre las moléculas.
5. El promedio de energía cinética de una molécula es de 3kT/2 (siendo T la temperatura absoluta y k la constante de Boltzmann).

¿Qué significan estos postulados?

Según el modelo cinético molecular que se toma como válido hoy en día, como decíamos, todo material que vemos está formado por partículas muy pequeñas llamadas moléculas. Estas moléculas están en movimiento continuo y se encuentran unidas por la fuerza de cohesión que existe entre moléculas de una misma materia. Entre una y otra hay un espacio vacío, ya que están en continuo movimiento.

Cuando las moléculas están muy juntas y se mueven en una posición fija, las fuerzas de cohesión son muy grandes. Es el estado sólido de la materia. En cambio cuando están algo más separadas y la fuerza de cohesión es menor, lo que les permite cambiar de posición libremente de forma independiente, estamos en presencia de un líquido.

En el estado gaseoso, las moléculas están totalmente separadas unas de otras y se mueven libremente. Aquí no existe fuerza de cohesión.

Teoría Cinética de los Gases

Los cuerpos en la Naturaleza se nos presentan en tres estados de agregación molecular: gaseoso, líquido y sólido. El primer autor que empleó la palabra “gas”, fue el belga VAN HELMONT (1577-1644), quién la aplicó a “espíritus desconocidos” producidos al quemar la madera. Un “gas” es la materia que posee la propiedad de llenar completamente un recipiente a una densidad uniforme.

El fenómeno de la difusión constituye una importante prueba en apoyo de la fecunda teoría de que la materia está constituida por partículas pequeñísimas llamadas moléculas, cuyo movimiento permanete es la causa de la difusión.

TEORIA CINETICA DE LOS GASES

La Teoría Cinética de los Gases explica el comportamiento de los gases utilizando un “modelo” teórico. Suministra un modelo mecánico el cual exhibe propiedades mecánicas promedias , que están identificadas con propiedades macroscópicas, es decir que impresionan nuestros sentidos, tales como la presión. En este modelo , una sustancia gaseosa pura consiste del agregado de un número muy grande de partículas independientes llamadas moléculas, que son muy pequeñas, perfectamente elásticas y están moviendose en todas direcciones.

El primer intento para explicar las propiedades de los gases desde un punto de vista puramente mecánico, débese a BERNOULLI (1738)Sin embargo no adquirió mayor importancia hasta la mitad del siglo XIX, cuando CLASIUS utilizó el movimiento de las moléculas para relacionar la energía mecánica con el calor. Debido a la labor de CLASIUS, MAXWELL, BOLTZMANN, VAN DER WAALS, las ideas primitivas fueron desarrolladas y se dio forma matemática a la Teoría Cinética de los Gases. Los postulados de esta teoría son los siguientes:

·  Los gases están constituidos de partículas discretas muy pequeñas, llamadas moléculas. Para un determinado gas, todas sus moléculas son de la misma masa y tamaño, que difieren según la naturaleza del gas. Como un ejemplo, en 1 cm3 de aire hay 25 trillones de moléculas.

·  Las moléculas de un gas que se encuentren dentro de un recipiente, están dotadas de un movimiento incesante y caótico, como resultado del cual chocan frecuentemente entre sí y con las paredes del recipiente que las contiene.

·  La presión de un gas es le resultado de las colisiones de las moléculas contra las paredes del recipiente es idéntica sobre todas las paredes.

·  Si se obliga a las moléculas de un gas a ocupar un recipiente mas pequeño, cada unidad del área del recipiente recibirá un numero mayor de colisiones, es decir que aumentara la presión del gas.

·  Cuando se guarda una cantidad de un gas indefinidamente en un recipiente cerrado, a temperatura constante, la presión no disminuye con el tiempo, mientras no haya un escape del gas. Al respecto se sabe que este gas no absorbe calor de continuo del exterior para suministrar la energía de movimiento de las moléculas. Todo esto es verdad solamente si las moléculas son perfectamente elásticas en el choque de unas contra otras. Es de recordar que CLASIUS comparo las moléculas a bolas de billar.

·  Bajo las condiciones ordinarias de presión y temperatura, el espacio ocupado propiamente por las moléculas dentro de un volumen gaseoso, es una fracción muy pequeña del volumen de todo el gas. Ahora desde que las moléculas son muy pequeñas en comparación a las distancias entre ellas, pueden ser consideradas en primera aproximación como puntos materiales.

·  La temperatura absoluta de un gas es una cantidad proporcional a la energía cinética promedio de todas las moléculas de un sistema gaseoso. Un aumento en la temperatura del gas originara un movimiento mas poderoso de las moléculas, de tal modo que si mantiene el volumen constante, aumentara la presión de dicho gas. 

Historia De la Teoría Cinético-Molecular

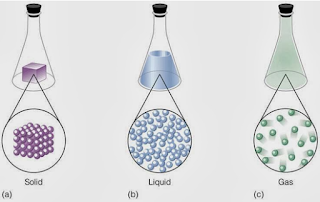
La identificación definitiva del fenómeno del calor con el movimiento se realiza en la teoría cinético-molecular de los gases, como un conjunto de partículas o moléculas  en movimiento de acuerdo con la teoría atómica de la materia. Daniel Bernoulli decía que el movimiento de las partículas de un gas podía explicar su presión y temperatura. Lo propuso en 1738 en su Hidrodinámica.

Hacia 1848 Joule había presentado un trabajo sobre la teoría cinética de los gases.  Joule consideró un gas formado por moléculas confinadas en cierto volumen que se movían con cierta velocidad pero que no colisionaban entre sí. De esta forma la presión viene dada por el choque elástico de las moléculas con las paredes del volumen y la temperatura es una medida de la velocidad de las moléculas con las paredes del volumen y la temperatura es una medida de la velocidad de las moléculas.

 

 Clausius, hacia 1857, ya había formulado matemáticamente la teoría cinética de los gases, sin explicar la estadística, establecía que las velocidades de las partículas de un gas debían variar mucho entre sí.

James C. Maxwell (1831-1879) es considerado uno de los grandes físicos por sus contribuciones a la termodinámica y al electromagnetismo. Su aportación principal a la termodinámica consistió en la aplicación de la estadística a la teoría cinética de los gases, contenida en Illustrations of dynamical theory of gases (1860, Ilustraciones de la teoría dinámica de los gases). En esta obra Maxwell propuso que las propiedades de un gas se pueden deducir del movimiento de sus partículas.

Maxwell propuso por primera vez una expresión para la distribución estadística de las velocidades de las moléculas de un gas. El número de moléculas (n) de masa (m) contenido en un elemento de volumen (dV), cuya velocidad es cercana a una dada (v) tiene una distribución exponencial.

Donde “k” es una constante, llamada constante de Boltzmann, igual a 1,38x10-23 j/°k

Maxwell estudio también las colisiones entre las moléculas  y su relación con la viscosidad.

En 1871 propuso, llamado por Kelvin el “Demonio de Maxwell” que situado entre dos compartimientos de un gas que están inicialmente a la misma temperatura, deja pasar solo a las partículas rápidas en una dirección, separando así a las rápidas de las lentas y produciendo que un compartimiento se caliente y el otro se enfríe. Esto parece violar la segunda ley de la termodinámica, ya que aparentemente sin gastar energía el estado final está más ordenado que el inicial.

Ludwin E. Boltzmann (1844-1906) Sus contribuciones a la teoría cinética de los gases decía que el desarrollo de la distribución estadística de la energía de un gas entre sus moléculas, presentada también por Maxwell, y conocida con los dos nombres.

Boltzmann propuso por primera vez en 1877 en su obra Über die Bezieung zwischen dem Zweiten Hauptsatze der mechanischen Wärmtheorie und der Warhrscheinlichkeitregnung (Sobre la relación entre la segunda ley de la teoría mecánica del calor y el calcula de probabilidades) que el concepto de entropía es la medida del desorden de un sistema. Partió de la idea de que un sistema macroscópico está formado por un conjunto de partículas, en principio, puede estar en cualquier estado.

En este sentido relaciono la entropía con la probabilidad de que un sistema esté en un estado determinado, expresándolo con la ecuación, que después de su muerte se grabaría en su tumba (S=k log p+b, donde p es la probabilidad de que el sistema esté en un estado determinado y K la constante que hoy lleva su nombre). L entropía crece con la probabilidad yes un índice del desorden del sistema.

De acuerdo con Boltzmann, el pasar de un estado de desorden a uno de orden, sin aportación de energía desde afuera del sistema, no es estrictamente imposible, sino enormemente imposible. A partir de esta interpretación, la entropía se puede aplicar a muchos otros procesos además de los térmicos, que estén relacionados con el orden y el desorden. 

 Entre  las primeras aplicaciones de la estadística aplicaciones de la estadística a los problemas de la termodinámica se encuentran, también, los trabajos de Gibbs quien puso las bases de la mecánica estadística en su obra  Elementary principles of stadistical mechanics (1902, principios elementales de la mecánica estadística).

Gibbs propuso en 1901 expresiones para la probabilidad de que un sistema se encuentre en un estado de energía dado, generalizando una expresión hallada por Boltzmann en 1868.

La mecánica estadística, con las siguientes aportaciones, entre ellas las de Planck y las de Einstein, constituye hoy un importante instrumento de la física, aplicable tanto a sistemas clásicos como cuánticos.